During the year you probably did some driving, hiking, or flying. You may have traveled ‘over the river and through the woods to grandmother’s house‘ and back home without getting lost. A voice might have been telling you when and where to turn just when you needed it. Your phone might have been smart enough to locate you and direct you to your destination.
GPS devices are ubiquitous. We take them for granted and don’t think much about them. They are a remarkable piece of technology with applications in many areas. Our son-in-law uses it while farming. During harvest, GPS records his field position and associates it with the yield. This information is overlaid onto his field maps with GIS (Geographic Information System). Soil testing uses GPS mapping to see which field areas need chemicals. Insect infestations can be mapped with GPS. Truck spreaders or airplane sprayers can follow the GPS maps for precisely located applications.
GPS is used for fire, ambulance, police, search and rescue, trucking, delivery vehicles, and public transportation. Recreational uses of GPS include navigation while hiking, hunting, skiing, and on golf courses to track golf carts, and to let players know how far it is to the center of the greens. GPS is being used for recreational sailing and fishing and for commercial shipping fleet management. In the air, GPS is being used for en-route navigation, aircraft landing, and air-collision avoidance systems. New applications of the technology are being developed all the time.
Do you have any idea how GPS locates you? It is actually quite simple in concept, but complex in practice. This post focuses on the simple concepts. But, it isn’t quite as simple as xkcd imagines.
The Constellation of Satellites |
The Global Positioning System (GPS) primarily consists of 24 active satellites with several more in reserve and in orbit. There were 31 in orbit as of 2011. They are made by Rockwell, Boeing, and Lockheed Martin. Older satellites are replaced with newer ones when needed. Some satellites are over 20 years old. The reserve satellites are in positions to be readily available.
The GPS constellation delivers consistently high performance due to the dedicated efforts of its operators — the men and women of the U.S. Air Force. The 2nd Space Operations Squadron at Schriever Air Force Base in Colorado Springs, Colorado, is responsible for the daily command and control of the GPS constellation. The squadron ensures continuous GPS availability and high accuracy to millions of users, both military and civilian, on a 24/7 basis.
Characteristics of the satellite constellation..
- Orbits are circular
- Period of orbit is 12 hours
- Altitude of orbit is 12,500 miles
- Six orbital planes inclined 55˚ to the equator
- Four satellites per orbit with reserves in some
Standard Positioning Service (SPS) provides the data for the general consumer. With 4 or more satellites acquired, the delivered signal can provide accuracy of within 7.8 meters 95% of the time. The actual accuracy end users can expect depends on factors outside the government’s control, including atmospheric effects and receiver quality. Some high-quality GPS SPS receivers can at times attain better than 3 meter horizontal position accuracy.
For nominal performance, GPS satellites need to be higher than about 25˚ above the horizon in order for the ground based mobile unit to ‘see’ and securely lock onto the signal. The mobile unit needs to access 4 or more satellites. This is usually not a problem. Sometimes as many as 9 satellites are accessed depending on conditions on the ground. The following 5 minute video has some good animations illustrating GPS access by a ground mobile unit in Los Angeles. You will see how the number and directions of satellite signals acquired is constantly changing.
The GPS system can calculate speed, direction, and estimated time of arrival. All of this is done by a constellation of satellites moving several thousand miles/hour and involving users who might also be moving at high rates of speed. How does the system locates the user on the ground and define a position horizontally and vertically? The key to plotting position lies in combining the simple relationship of distance = rate x time with the procedure of Trilateration in 3-D. First, consider the simpler case of Trilateration in 2-D. Then, extend that concept to 3-D.
Trilateration in 2-D |
Imagine the following situation. You are traveling with three friends in a car. For several hours, you have been in a profoundly deep sleep. Your three friends decide to play a practical joke on you, knowing you will sleep like a log for a very long time. They deposit you in a motel room in some small town with no identifying information in view about your location. They hide all of your clothes except for your underwear. They leave you a cell phone and a big U.S. map, ruler, and a drawing compass. When you wake up, you want to find out where you are located. But, it is -25˚F outside, You can’t leave the room in your underwear. So, you call friend #1. He answers and you yell at him in anger. He says “Cheer up. This is a puzzle to solve.” He says you are 720 miles from Casper, WY. You draw a circle on the map that big.
That doesn’t help much. You could be anywhere on that circle. So, you call friend #2. You yell at her. She also says to cheer up and says you are 555 miles from Fargo, ND. You draw another circle on the map that big.
That helps somewhat. You could be either in Canada or Iowa where the two circles intersect. But, how is that supposed to cheer you up? You call friend #3 and read him the riot act. He also says to cheer up. He says his clue should help you solve the puzzle and know your location. Once you do, they will tell you where to find your clothes and how to get home. He says you are 280 miles from Wausau, WI. Hurriedly you draw the circle on the map centered on Wausau. Bingo! Where the three known distances intersect is your location.
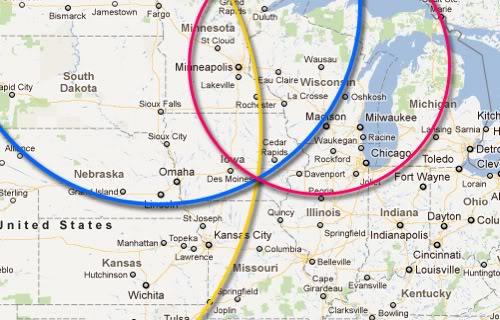
You peer in closer to the map and check the name of the town in Iowa. “Very funny, guys!”
Trilateration in 3-D |
That silly example is designed to show one thing. Once you know three accurate distances from three specific locations, it is an easy matter to plot their intersection on a two dimensional map. For satellites in space, orbiting a three dimensional Earth, the task is more challenging. GPS uses the intersection of four spheres instead of circles to define your location. In addition, there are sources of error which make the distances of the radii of the spheres to be inexact. Let’s examine what information is transmitted by each satellite.
For this part of the discussion, I am borrowing and modifying some graphics from an online article by Diana Cooksey, MSU GPS Laboratory, Department of Land Resources and Environmental Sciences, Montana State University-Bozeman.
Each satellite has an atomic clock on board. All of the clocks are kept synchronized by the 2nd Space Operations Squadron. They constantly transmit two kinds of signals to the ground. One radio signal is called an ephemeris. It contains a unique code that identifies the satellite. The signal also tells the location of the satellite. Clock behavior and any clock corrections, and GPS system time are included. The time is coded so the receiver knows when it was transmitted. The receiver clock is synchronized with the satellite clock. Signal transmission takes about 0.06 seconds to reach the receiver.
When the time of the received signals are compared to the code telling when the signal was sent, there is a time difference between them. By multiplying the time difference by the speed of light, the receiver calculates the distance to the satellite at that time.
An almanac is also transmitted telling the ground unit the approximate location data for each of the 24 active satellites. The almanac is automatically downloaded and takes several minutes to be received.
Signal From Satellite 1
As each moment passes, your GPS unit should be receiving at least 4 signals. Let’s consider the information obtained from the first satellite of the four. The ground unit is located in this example where the yellow dot shows on the Earth, but it doesn’t know that for sure. The unit receives the time signal and computes the time difference from the time code method described above. For example, it might calculate a distance of 12,000 miles. Distance = speed of light x time diff. The GPS unit ‘thinks’ its location could be anywhere on the surface of that large sphere based on only knowing it is 12,000 miles from the satellite.
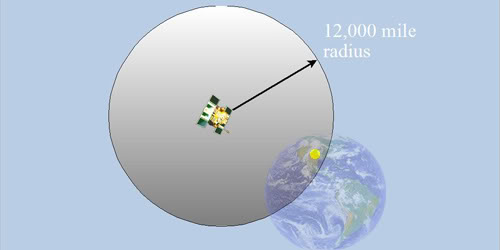
Signal From Satellite 2
The GPS unit also receives a signal from a second satellite. The time delay is used to calculate a radius of the second sphere. It might get a value this time of 11,000 miles. Now the GPS unit ‘thinks’ it could be on any of the points that are both 12,000 miles from #1 and 11,000 miles from #2. That intersection of spheres defines a circle. In the figure, the circle is viewed obliquely. We can see the yellow dot on the surface of the Earth is part of the circle. But, the GPS unit still doesn’t know for sure where it is located. It only ‘thinks’ its location could be at any point on the circle. But, that is an improvement.
Signal From Satellite 3
The signal from the third satellite might give a radius of 11,500 miles. This time the intersection of the circle and the surface of the third sphere includes only 2 points, marked as yellow dots. One of those is out in space and is discarded. The GPS unit ‘concludes’ it is on the surface of the Earth.
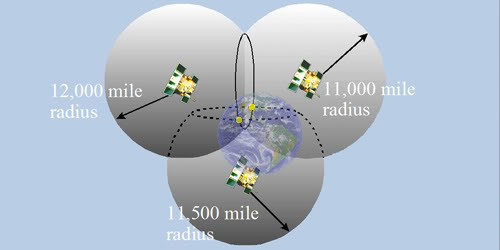
Why Do We Need Satellite 4?
Various factors introduce errors into the time difference calculation. The signal could reflect off of another nearby object. It refracts as it goes through the atmosphere. The speed of light is altered by air and water vapor. And, the clocks on the satellite and GPS unit are not perfectly in sync. There is a small timing offset. These factors cause a range of uncertainties in the time differences and in the resulting radial distance calculations. The speed of light is exceedingly fast. A time error of 1 billionth of a second results in a distance error of about a foot. The intersection of the surfaces of the three spheres is not sharp and exact. The intersection is a ‘fuzzy’ volume of space several tens of meters across.
The fourth satellite signal sphere intersects with the first three. The GPS unit uses this additional radius to rapidly calculate an adjustment factor for all 4 of the radii. This adjustment lets the intersection of all four spheres pass as near as possible through one point. Doing so more accurately defines the position within a few meters both horizontally and vertically.
Since this is an ongoing process in time, changes to that position with respect to time are used to calculate speed and direction of travel. These values are used in concert with the database of maps and highways to compute travel times and arrival times.
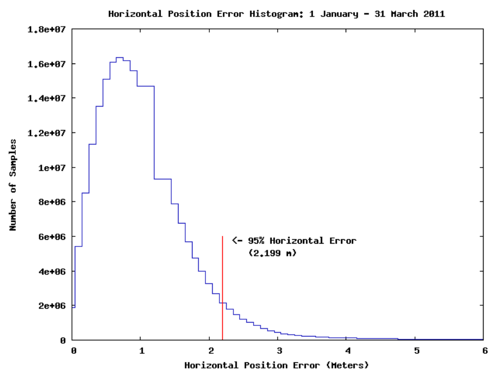
FAA data collected in early 2011 shows that the horizontal accuracy of GPS SPS is often within 1 meter.
Accuracy of GPS |
GPS satellites broadcast position and timing data on two radio frequencies, L1 and L2. Two kinds of code are broadcast on the L1 frequency, C/A code and P code. Coarse Acquisition C/A code is available to civilian GPS users and provides Standard Positioning Service (SPS). Precise P code is broadcast on both the L1 and L2 frequencies. P code, used for the Precise Positioning Service (PPS), is available only to users with an authorized decoding key, such as the military. From the GPS.gov site…
The accuracy of the GPS signal in space is actually the same for both the civilian GPS service (SPS) and the military GPS service (PPS). However, SPS uses only one frequency, while PPS uses two. This means military users can perform ionospheric correction, a technique that reduces radio degradation caused by the Earth’s atmosphere. With less degradation, PPS provides better accuracy than the basic SPS.
From the Purdue University School of Technology, they discuss GPS accuracy in terms of surveying.
The GPS equipment will potentially maintain an accuracy of 5 millimeters, even when performing measurements over several miles. GPS equipment’s level of accuracy at great ranges is especially useful on extremely large construction projects, such as an airport project including runways, or on highway construction projects covering hundreds of miles.
Comments and More Technical Information |
My goal for this post was to give those who are interested in science and technology a better understanding of how GPS is able to determine their location. In doing so, I have learned a lot. I hope I have come close to reaching that goal for most of you. In doing the research, I realized how I have barely touched the surface of the technologies that are in effect making it all happen. For those of you who are more capable and curious, here are a few sources with more technical information that I chose not to include in the post.
http://www.gps.gov/
http://www.nstb.tc.faa.gov/
http://what-when-how.com/…
http://hubtechinsider.wordpress.com/…
http://www.tomtom.com/…
Video of GPS use for aircraft navigation from the FAA
The next time you drive, fly, hike, and use a GPS unit, give some thought to how these units constantly monitor your position. Consider the technology that enables them to locate you within a few meters anywhere on the Earth. Safe travels.
How I See It 
Interesting … I had no clue how it worked, and found it interesting that multiple satellites are involved. The silly story was a good example of how it works.
Thank you, Frank. I had fun with it.
I learned a lot about the technology.